Schießen im Hochgebirge – Mythos Winkelschuss - part 2

Jeder kennt die verschiedenen bergauf/bergrunter –Sprüche aus der Jägerschaft. In der jagdlichen Welt existiert darüber sehr viel gefährliches Halbwissen und gern wird am Stammtisch so manches „Wissen“ herumgereicht. Genau betrachtet, basiert der Schuss im Winkel jedoch auf einfachen physikalischen Grundlagen. Im folgenden Artikel möchten wir mit dem Mythos Winkelschuss aufräumen und die Schießlehre für den Schuss in steilen Winkeln erklären. Im Grunde genommen ist Schießen in der Theorie nicht schwer, denn es ist reine Physik und basiert auf mathematischen Grundsätzen, die jedem hinlänglich aus der Schule bekannt sein müssten. Mit dem Winkelschuss ist dies natürlich genauso:

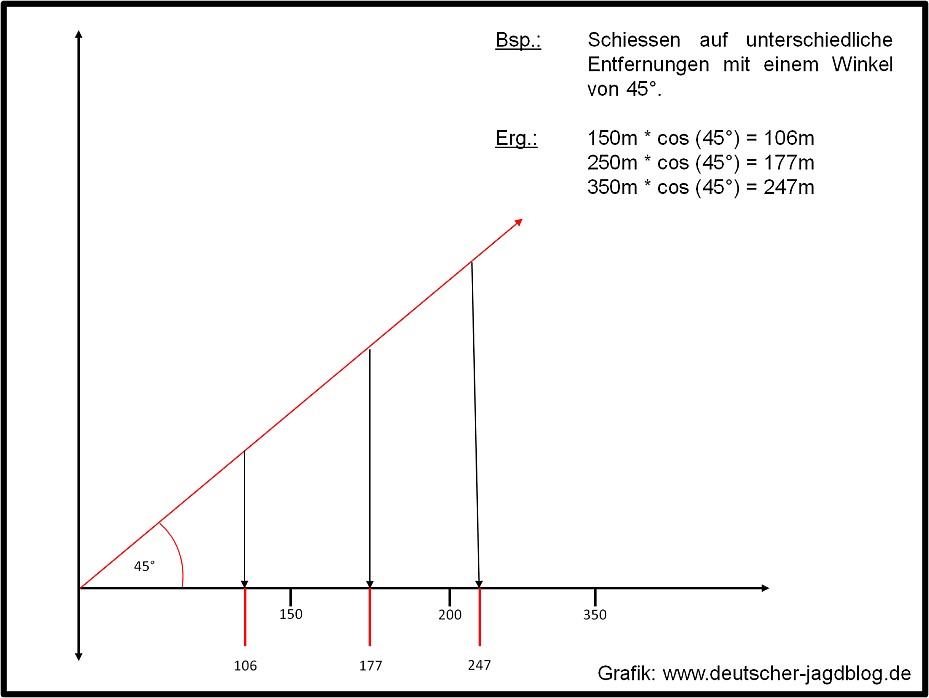
Es gibt mehrere Modelle zur Erklärung des steilen Schusses. Die populärste Theorie, auf der auch die meisten Ballistikrechner basieren, ist die „Rifleman-Rule“ oder „Sniperchoice“. Diese besagt, bei einem Winkelschuss verkürzt man die Strecke auf der die Schwerkraft auf das Projektil einwirken kann, wodurch das Geschoss eine kürzere Strecke fliegt. Am besten kann man sich dieses physikalische Phänomen veranschaulichen, indem man zu Hause den Gartenschlauch nimmt und in unterschiedlichen Winkeln das Beet bewässert. Man wird feststellen, dass bei einem Winkel von 45° das Wasser am weitesten spritzt und das Wasser in einer parabelförmigen Flugbahn seinen Weg nimmt. Die relative Entfernung zum Boden, die das Wasser dabei zurück legt, ist daher stets kürzer als die Strecke der Flugbahn.

Grundlagen

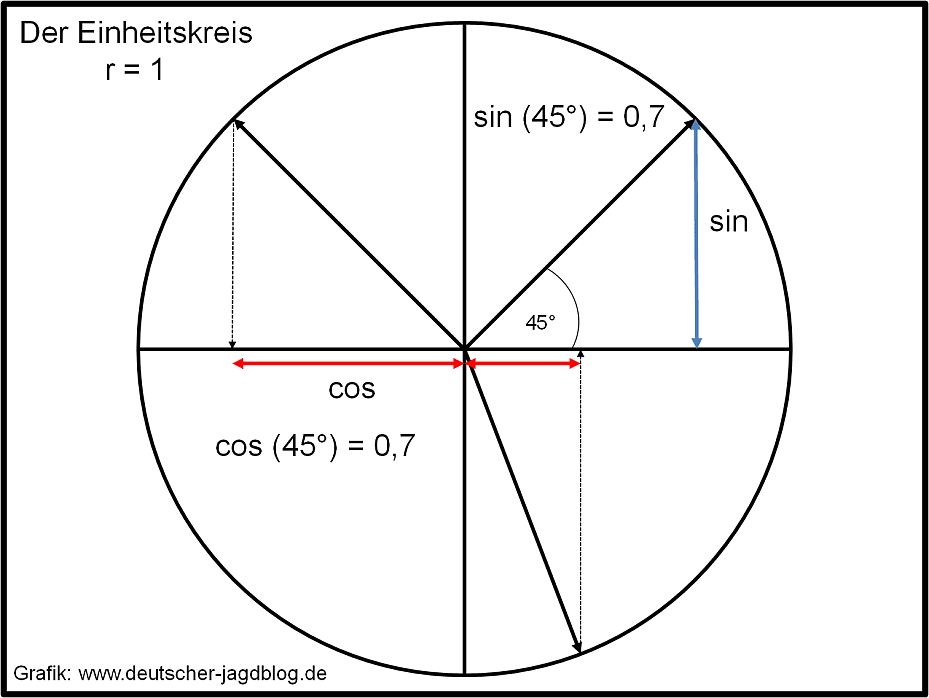
Am einfachsten lässt sich der Winkelschuss mit dem mathematischen Einheitskreis erklären. Keine Sorge wir werden die Berechnung des Sinus und Cosinus nicht herleiten – wir setzen einfach mal voraus, dass jeder grundlegend mit der Thematik vertraut sein sollte.

Der mathematische Einheitskreis ist ein größenunabhängiger Kreis mit dem Radius 1. Auf der Abbildung 1 haben wir zur Veranschaulichung einen solchen Kreis gezeichnet und in vier Teile unterteilt. Zieht man nun eine Verbindung vom Mittelpunkt des Kreises zur Außenkante und fällt ein Lot zu einer der Linien, die den Kreis unterteilen, so kann man den Sinus bzw. den Cosinus wie in der Abbildung gezeigt, ablesen. Bei einem Winkel von 45° sind der Sinus und Cosinus gleich. Für den Winkelschuss ist lediglich der Cosinus relevant, da er relativ zur Waagerechten berechnet wird. In der Realität müssen wir den Sinus und Cosinus nicht umständlich über eine solche Grafik ableiten, Scharfschützen benutzen hierfür z. B. Winkeltabellen.

Um nun die relative Entfernung zu einem Ziel zu berechnen, muss man also den Winkel kennen, mit dem man schießt und man muss die Entfernung zum Ziel kennen. Angenommen, man möchte eine Gams auf 150 m in einem Winkel von 45° schießen, dann nehme man einen Taschenrechner und drücke 45 cosvund multipliziert dann diesen Wert mit der realgemessenen Entfernung zur Gams. Als Hilfsmittel bietet sich dafür ein Laserentfernungsmesser an. Alternativ kann man auch den Cosinus von einer Libelle ablesen oder den entsprechenden Wert aus unserer Tabelle entnehmen. In der Abbildung 2 haben wir die Berechnungen für die Entfernungen 150 m, 250 m und 350 m mit einem Winkel von 45° beispielhaft vorgegeben. Die Ergebnisse können hier leicht verständlich abgelesen werden.